이제 모델을 테스트 데이터에 적용하여 각 모델의 예측 성능을 비교할 수 있습니다. 의사 결정 트리 모델이 과다 적합(over-fitting)되어 만들어 진 것이 맞다면, 다른 두 모델과 비교하여 테스트 데이터에서도 예측 결과가 잘못 형성되는 것을 확인할 수 있어야 합니다. 랜덤 포리스트가 선형 모델에서는 누락되어 있는 데이터의 일부 고유 신호를 포착한다고 생각된다면, 테스트 데이터에서 선형 모델보다 성능이 우수한 모습을 확인할 수 있어야 합니다.
살펴볼 첫 번째 측정 기준은 제곱된 잔차의 평균(the average of the squared residuals)입니다. 이 값을 통하여 예측값이 관측값과 얼마나 가까운 지를 알 수 있습니다. 일반적으로 0% ~ 20%의 좁은 범위에 있는 팁 비율을 예측하기 때문에, 좋은 모델은 잔차가 평균 2 ~ 3 % 포인트를 넘지 않아야 할 것으로 예상해야 합니다.
rxPredict(trained.models$linmod, data = mht_split$test, outData = mht_split$test, predVarNames = "tip_percent_pred_linmod", overwrite = TRUE)
rxPredict(trained.models$dtree, data = mht_split$test, outData = mht_split$test, predVarNames = "tip_percent_pred_dtree", overwrite = TRUE)
rxPredict(trained.models$dforest, data = mht_split$test, outData = mht_split$test, predVarNames = "tip_percent_pred_dforest", overwrite = TRUE)
rxSummary(~ SE_linmod + SE_dtree + SE_dforest, data = mht_split$test,
transforms = list(SE_linmod = (tip_percent - tip_percent_pred_linmod)^2,
SE_dtree = (tip_percent - tip_percent_pred_dtree)^2,
SE_dforest = (tip_percent - tip_percent_pred_dforest)^2))
Call:
rxSummary(formula = ~ SE_linmod + SE_dtree + SE_dforest, data = mht_split$test,
transforms = list(SE_linmod = (tip_percent - tip_percent_pred_linmod)^2,
SE_dtree = (tip_percent - tip_percent_pred_dtree)^2,
SE_dforest = (tip_percent - tip_percent_pred_dforest)^2))
Summary Statistics Results for: ~SSE_linmod + SSE_dtree + SSE_dforest
Data: mht_split$test (RxXdfData Data Source)
File name: C:\Data\NYC_taxi\output\split\train.split.train.xdf
Number of valid observations: 43118543
Name Mean StdDev Min Max ValidObs MissingObs
SE_linmod 82.66458 108.9904 0.00000000005739206 9034.665 43118542 1
SE_dtree 82.40040 109.1038 0.00000251589457986 8940.693 43118542 1
SE_dforest 82.47107 108.0416 0.00000000001590368 8606.201 43118542 1
살펴볼 가치가 있는 또 다른 측정 기준은 상관 행렬(correlation matrix)입니다. 이는 서로 다른 모델의 예측이 어느 정도 서로 가깝고 어느 정도까지 실제 또는 관찰된 팁 비율에 근접하는지를 판단하는 데 도움이 될 수 있습니다.
rxc <- rxCor( ~ tip_percent + tip_percent_pred_linmod + tip_percent_pred_dtree + tip_percent_pred_dforest, data = mht_split$test)
print(rxc)
tip_percent pred_linmod pred_dtree pred_dforest
tip_percent 1.0000000 0.1391751 0.1500126 0.1499031
tip_percent_pred_linmod 0.1391751 1.0000000 0.8580617 0.9084119
tip_percent_pred_dtree 0.1500126 0.8580617 1.0000000 0.9404640
tip_percent_pred_dforest 0.1499031 0.9084119 0.9404640 1.0000000
예측 결과 비교
알고리즘을 테스트 데이터에 적용하기에 앞서서, 모든 범주형(categorical) 변수들의 조합으로 작은 데이터 세트에 알고리즘을 적용하고, 예측 결과를 시각화 합니다. 이것은 우리가 각각 알고리즘에 대한 직관을 발전시키는 것에 도움이 될 것입니다.
pred_df <- expand.grid(ll)
pred_df_1 <- rxPredict(trained.models$linmod, data = pred_df, predVarNames = "pred_linmod")
pred_df_2 <- rxPredict(trained.models$dtree, data = pred_df, predVarNames = "pred_dtree")
pred_df_3 <- rxPredict(trained.models$dforest, data = pred_df, predVarNames = "pred_dforest")
pred_df <- do.call(cbind, list(pred_df, pred_df_1, pred_df_2, pred_df_3))
head(pred_df)
pickup_nb dropoff_nb pickup_hour pickup_dow pred_linmod pred_dtree pred_dforest
1 Chinatown Chinatown 1AM-5AM Sun 6.869645 5.772054 9.008643
2 Little Italy Chinatown 1AM-5AM Sun 10.627190 9.221250 10.634590
3 Tribeca Chinatown 1AM-5AM Sun 9.063741 9.221250 10.099731
4 Soho Chinatown 1AM-5AM Sun 10.107815 8.313437 10.162946
5 Lower East Side Chinatown 1AM-5AM Sun 9.728399 9.221250 10.525242
6 Financial District Chinatown 1AM-5AM Sun 8.248997 6.937500 8.674807
observed_df <- rxSummary(tip_percent ~ pickup_nb:dropoff_nb:pickup_dow:pickup_hour, mht_xdf)
observed_df <- observed_df$categorical[[1]][ , c(2:6)]
pred_df <- inner_join(pred_df, observed_df, by = names(pred_df)[1:4])
ggplot(data = pred_df) +
geom_density(aes(x = Means, col = "observed average")) +
geom_density(aes(x = pred_linmod, col = "linmod")) +
geom_density(aes(x = pred_dtree, col = "dtree")) +
geom_density(aes(x = pred_dforest, col = "dforest")) +
xlim(-1, 30) +
xlab("tip percent")
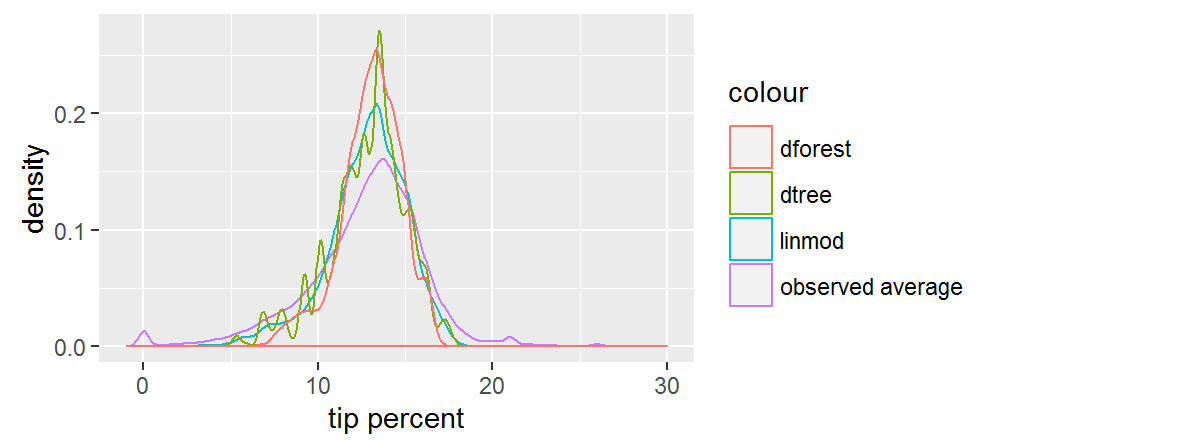
선형 모델과 랜덤 포레스트 모델은 둘 모두 우리에게 부드러운 곡선의 예측을 제공합니다. 우리는 랜덤 포레스트 예측이 가장 중앙 집중되어 있음을 알 수 있습니다. 의사 결정 트리에 대한 예측은 아마도 과다 적합(overfitting)의 결과로 인한 들쭉날쭉 한 분포를 따르지만, 우리가 테스트 세트에 대하여 성능을 확인하기 이전까지는 정말 이런 모습인지를 알 수 없습니다. 전체적으로, 예측 결과들은 측정된 평균보다 폭이 더 좁습니다.
다른 알고리즘 사용
지금까지 동일한 rxLinMod 알고리즘을 사용하는 두 모델을 살펴 보았습니다. 이 둘을 비교하면서, 우리는 모델을 만드는 데 사용된 변수들이 각각의 예측에 미치는 영향도를 포착하는 방법을 살펴 보았습니다. 이러한 비교를 위해서, 모델을 만드는 데 사용되는 모든 변수들의 조합을 사용하여 데이터 세트를 만들고, rxPredict를 사용하여 두 모델로 해당 데이터 세트에 대하여 스코어링을 수행하였습니다. 그렇게 함으로써 우리는 예측이 어떻게 분포되어 있는지를 알 수는 있습니다만 ,그러나 여전이 이러한 예측이 옳은지는 아직 알 수가 없습니다. 모델의 성능에 대한 진정한 테스트는 샘플 데이터 이외의 자료에 대하여 예측할 수 있는 능력에 있습니다. 따라서 우리는 데이터를 두 개로 나누고, 모델의 테스트를 위해 한 부분을 따로 보관 합니다.
데이터를 트레이닝과 테스트의 두 부분으로 나누기 위해, 먼저 rxDataStep을 사용하여 split이라는 새 factor 열을 작성하였습니다. 이 열에는 "train"또는 "test" 값이 부여되어, 이를 통하여 주어진 데이터 비율(여기서는 75 %)이 모델 트레이닝에, 나머지는 모델의 예측 능력을 테스트하는 데 사용됩니다. 이어서 rxSplit 함수를 사용하여 데이터를 두 부분으로 나눕니다. 여기에서 우리가 만드는 rx_split_xdf 함수는 앞서의 두 단계를 하나로 결합하고, 일부 인수들에 대하여 기본값을 설정합니다.
dir.create('output', showWarnings = FALSE)
rx_split_xdf <- function(xdf = mht_xdf,
split_perc = 0.75,
output_path = "output/split",
...) {
# first create a column to split by
outFile <- tempfile(fileext = 'xdf')
rxDataStep(inData = xdf,
outFile = xdf,
transforms = list(
split = factor(ifelse(rbinom(.rxNumRows, size = 1, prob = splitperc), "train", "test"))),
transformObjects = list(splitperc = split_perc),
overwrite = TRUE, ...)
# then split the data in two based on the column we just created
splitDS <- rxSplit(inData = xdf,
outFilesBase = file.path(output_path, "train"),
splitByFactor = "split",
overwrite = TRUE)
return(splitDS)
}
# we can now split to data in two
mht_split <- rx_split_xdf(xdf = mht_xdf, varsToKeep = c('payment_type', 'fare_amount', 'tip_amount', 'tip_percent', 'pickup_hour',
'pickup_dow', 'pickup_nb', 'dropoff_nb'))
names(mht_split) <- c("train", "test")
이제 데이터에 대해 세 가지의 다른 알고리즘을 실행합니다.
- rxLinMod, 앞서의 선형 모델이며 다음 인자를 사용 : tip_percent ~ pickup_nb:dropoff_nb + pickup_dow:pickup_hour
- rxDTree, 의사 결정 트리 알고리즘 : tip_percent ~ pickup_nb + dropoff_nb + pickup_dow + pickup_hour(factor간 조합 분석이 알고리즘 자체에 내장되어 있기 때문에 의사 결정 트리에는 조합 factor가 필요하지 않음)
- rxDForest, 랜덤 포리스트 알고리즘은 의사 결정 트리와 같은 인자를 사용
우리 코스는 모델링 과정이 아니기 때문에, 알고리즘 구현 방법에 대해서는 다루지 않을 것입니다. 대신 우리는 알고리��을 실행하고, 테스트 데이터의 팁 퍼센트를 예측하여, 어느 알고리즘이 더 효과적인지 알 수 있습니다.
system.time(linmod <- rxLinMod(tip_percent ~ pickup_nb:dropoff_nb + pickup_dow:pickup_hour,
data = mht_split$train, reportProgress = 0))
system.time(dtree <- rxDTree(tip_percent ~ pickup_nb + dropoff_nb + pickup_dow + pickup_hour,
data = mht_split$train, pruneCp = "auto", reportProgress = 0))
system.time(dforest <- rxDForest(tip_percent ~ pickup_nb + dropoff_nb + pickup_dow + pickup_hour,
mht_split$train, nTree = 10, importance = TRUE, useSparseCube = TRUE, reportProgress = 0))
user system elapsed
0.00 0.00 1.62
user system elapsed
0.03 0.00 778.00
user system elapsed
0.02 0.00 644.17
위의 알고리즘들은 실행하는 데 시간이 꽤 걸릴 수 있으므로, 각각의 반환된 모델을 저장하는 것이 좋습니다.
trained.models <- list(linmod = linmod, dtree = dtree, dforest = dforest)
save(trained.models, file = 'trained_models.Rdata')
여러 모델에서 선택
우리가 스스로 물어 보는 질문중 하나는 pickup_dow와 pickup_hour 사이의 상호 작용이 예측 결과에 얼마나 영향을 미치는가 입니다. pickup_nb와 dropoff_nb 사이의 상호 작용 내용만 유지하고 두 번째 상호 작용을 삭제하면 예상치는 얼마나 떨어질까요? 이를 알아보기 위해 우리는 pickup_nb:dropoff_nb만 포함하는 rxLinMod를 사용하여 보다 단순화 된 모델을 만들 수 있습니다. 만들어진 단순 모델로 만들어진 새로운 예측 결과를 cbind를 사용하여 보다 복잡한 모델로 작성한 기존 예측 데이터에 추가합니다.
form_2 <- as.formula(tip_percent ~ pickup_nb:dropoff_nb)
rxlm_2 <- rxLinMod(form_2, data = mht_xdf, dropFirst = TRUE, covCoef = TRUE)
pred_df_2 <- rxPredict(rxlm_2, data = pred_df_1, computeStdErrors = TRUE, writeModelVars = TRUE)
names(pred_df_2)[1:2] <- paste(c('tip_pred', 'tip_stderr'), 2, sep = "_")
pred_df <- pred_df_2 %>%
select(starts_with('tip_')) %>%
cbind(pred_df_1) %>%
arrange(pickup_nb, dropoff_nb, pickup_dow, pickup_hour) %>%
select(pickup_dow, pickup_hour, pickup_nb, dropoff_nb, starts_with('tip_pred_'))
head(pred_df)
pickup_dow pickup_hour pickup_nb dropoff_nb tip_pred_2 tip_pred_1
1 Sun 1AM-5AM Chinatown Chinatown 6.782043 6.796323
2 Sun 5AM-9AM Chinatown Chinatown 6.782043 5.880284
3 Sun 9AM-12PM Chinatown Chinatown 6.782043 6.103625
4 Sun 12PM-4PM Chinatown Chinatown 6.782043 5.913130
5 Sun 4PM-6PM Chinatown Chinatown 6.782043 6.121957
6 Sun 6PM-10PM Chinatown Chinatown 6.782043 6.642192
위의 결과를 통해 단순 모델의 예측 결과값은 탑승 지역과 하차 지역이 같은 조합의 모든 요일과 모든 시간에서 동일하다는 것을 알 수 있습니다. 반면에 기존의 보다 복잡한 모델에 의한 예측 결과값은 4가지 변수의 모든 조합에 대해 고유하게 나타납니다. 즉, pickup_dow:pickup_hour를 모델에 추가하면 예측 결과에 추가적인 변형값이 반영됩니다. 우리는 이 변형값에 중요한 신호가 포함되어 있는지 또는 이것이 어느 정도의 노이즈 값인 경우인지를 알고 싶습니다. 이에 대한 답을 얻기 위해, pickup_dow와 pickup_hour로 나누어서 두 예측의 분포를 비교합니다.
ggplot(data = pred_df) +
geom_density(aes(x = tip_pred_1, col = "complex")) +
geom_density(aes(x = tip_pred_2, col = "simple")) +
facet_grid(pickup_hour ~ pickup_dow)
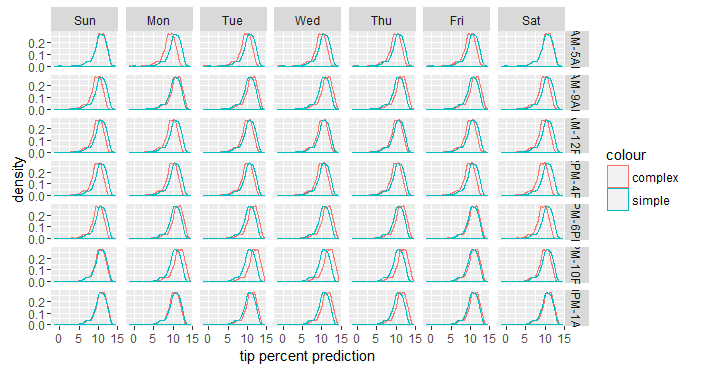
단순화 된 모델에 사용된 두 변수는 예측 결과값에 아무런 영향을 미치지 않기 때문에, 단순 모델은 전체적으로 동일한 분포를 보여 주지만, 더 복잡한 모델은 pickup_dow 및 pickup_hour의 각 조합에 대해, 일반적으로 분포가 조금 이동한 패턴으로, 약간 다른 분포를 보여줍니다 . 이러한 이동은 두 변수의 각 주어진 조합에서 pickup_dow 및 pickup_hour의 영향도를 나타냅니다. 이러한 이동은 방향성이 있기 때문에(우연이 아님) 중요한 신호(실제적인 중요성은 여전히 논쟁의 여지가 있지만)라고 단정하여도 이상이 없을 것입니다 . 만약 어떤 비즈니스 로직이 적용된다면, 단순화 된 내용을 선택할 수도 있습니다.
팁 예측값을 구간으로 나누어 봅시다. 구간값 선택에 참고하기 위해서, rxQuantile 함수를 사용할 수 있습니다.
rxQuantile("tip_percent", data = mht_xdf, probs = seq(0, 1, by = .05))
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 55% 60% 65% 70% 75% 80%
-1 0 0 0 0 0 0 0 9 12 15 17 17 17 18 18 19
85% 90% 95% 100%
20 21 23 99
위의 결과를 근거로 하여, 8% 미만, 8%~12%, 12%~15%, 15%~18%, 18% 이상인지 여부에 따라 tip_percent를 구분할 수 있습니다. 동일한 정보를 보여주는 막대 그래프를 그릴 수도 있으며, 이럴 경우 해석하기가 조금 더 쉽습니다.
pred_df %>%
mutate_at(vars(tip_pred_1, tip_pred_2), funs(cut(., c(-Inf, 8, 12, 15, 18, Inf)))) %>%
ggplot() +
geom_bar(aes(x = tip_pred_1, fill = "complex", alpha = .5)) +
geom_bar(aes(x = tip_pred_2, fill = "simple", alpha = .5)) +
facet_grid(pickup_hour ~ pickup_dow) +
xlab('tip percent prediction') +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
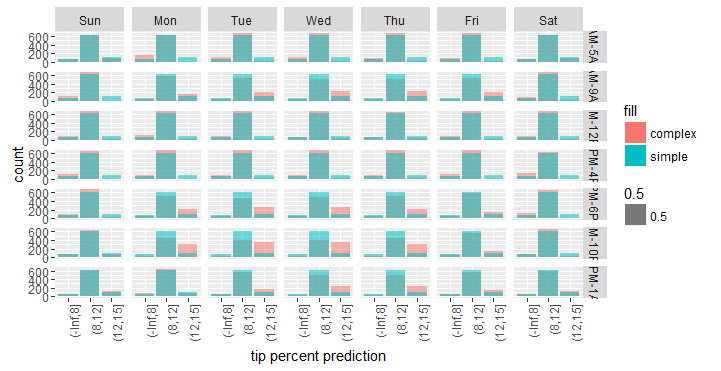
위의 그래프를 보면, 단순화 모델과 비교할 때 복잡한 모델은 특정 요일 및 시간 조합(예:월요일부터 목요일까지러시아워 시간대)에 더 높은 팁을 지불하는 승객과 평균보다 낮은 승객수를 예측하는 경향이 있음을 알 수 있습니다.
예측 결과 점검
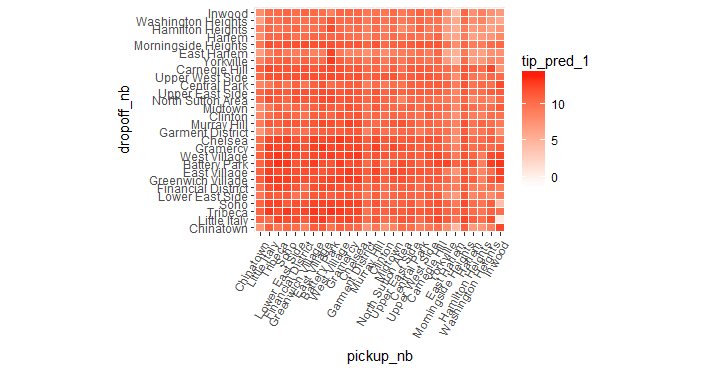
이제 모든 조합에 대한 예측 평균값을 플로팅하여 모델의 예측 결과를 시각화 할 수 있습니다.
ggplot(pred_df_1, aes(x = pickup_nb, y = dropoff_nb)) +
geom_tile(aes(fill = tip_pred_1), colour = "white") +
theme(axis.text.x = element_text(angle = 60, hjust = 1)) +
scale_fill_gradient(low = "white", high = "red") +
coord_fixed(ratio = .9)
ggplot(pred_df_1, aes(x = pickup_dow, y = pickup_hour)) +
geom_tile(aes(fill = tip_pred_1), colour = "white") +
theme(axis.text.x = element_text(angle = 60, hjust = 1)) +
scale_fill_gradient(low = "white", high = "red") +
coord_fixed(ratio = .9)
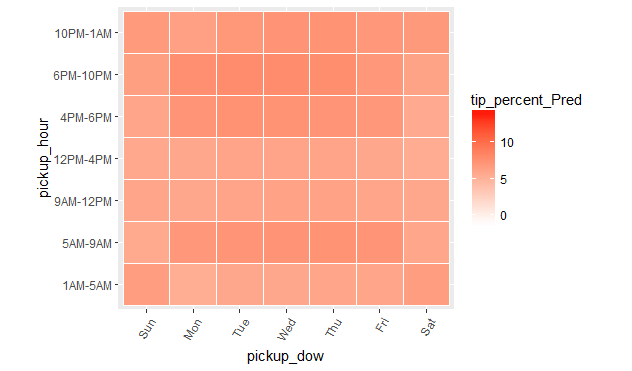
팁 비율을 예측하는 선형 모델(linear model)
하나는 pickup_nb와 dropoff_nb, 또 하나의 pickup_dow와 pickup_hour 사이에 상호작용 조건들를 포함하는 선형 모델을 만들어 보겠습니다. 여기에서 우리는 팁의 비율이 단순히 승객들이 어느 지역에서 승차했는지(pickup_nb), 어느 지역에서 하차 하였는지(dropoff_nb)가 아니라 승차와 하차의 쌍으로 부터 영향을 받는다는 것에 착안하였습니다. 또한 요일과 시간이 함께 팁에 영향을 미친다는 것을 추정 하였습니다. 예를 들어 일요일 9시 부터 12시 까지 사람들이 팁을 많이 준다는 것이, 모든 요일의 9시에서 12시 사이에는 높은 팁을 준다 또는 일요일이라면 언제라도 높은 팁을 준다 라는 것을 의미하지는 않습니다. 이러한 직관은 다음과 같이 rxLinMod 함수에 넘겨주는 모델 수식 인수로 인코딩됩니다.
tip_percent ~ pickup_nb : dropoff_nb + pickup_dow : pickup_hour
여기서 우리는 :을 사용하여 상호 작용 부분을 식별하고, +를 사용하여 추가 부분를 구분합니다.
form_1 <- as.formula(tip_percent ~ pickup_nb:dropoff_nb + pickup_dow:pickup_hour)
rxlm_1 <- rxLinMod(form_1, data = mht_xdf, dropFirst = TRUE, covCoef = TRUE)
모델 계수들(model coefficients)을 개별적으로 검사하는 것은 항목이 매우 많기 때문에 어려운 작업입니다. 또한 큰 데이터 세트를 사용하여 작업하는 경우, 표본의 크기가 크기 때문에, 실제로 큰 의미를 갖지 않지만 통계적으로 유의미한 것으로 나타나는 계수들이 많습니다. 따라서 여기에서는 우리의 예측이 어떻게 나타나는지를 살펴보기만 하겠습니다. 먼저 각각 변수들을 factor level의 list로 추출하여 expand.grid로 전달하여, 모든 가능한 factor level의 조합으로 데이터 집합을 만듭니다. 그런 다음 rxPredict를 사용하는 위 모델을 적용하여 tip_percent를 예측합니다.
rxs <- rxSummary( ~ pickup_nb + dropoff_nb + pickup_hour + pickup_dow, mht_xdf)
ll <- lapply(rxs$categorical, function(x) x[ , 1])
names(ll) <- c('pickup_nb', 'dropoff_nb', 'pickup_hour', 'pickup_dow')
pred_df_1 <- expand.grid(ll)
pred_df_1 <- rxPredict(rxlm_1, data = pred_df_1, computeStdErrors = TRUE, writeModelVars = TRUE)
names(pred_df_1)[1:2] <- paste(c('tip_pred', 'tip_stderr'), 1, sep = "_")
head(pred_df_1, 10)
tip_pred_1 tip_stderr_1 pickup_nb dropoff_nb pickup_dow pickup_hour
1 6.796323 0.16432197 Chinatown Chinatown Sun 1AM-5AM
2 10.741766 0.15853956 Little Italy Chinatown Sun 1AM-5AM
3 9.150114 0.09162002 Tribeca Chinatown Sun 1AM-5AM
4 10.174307 0.09819651 Soho Chinatown Sun 1AM-5AM
5 9.706202 0.07365164 Lower East Side Chinatown Sun 1AM-5AM
6 8.475197 0.06354026 Financial District Chinatown Sun 1AM-5AM
7 10.866035 0.07150005 Greenwich Village Chinatown Sun 1AM-5AM
8 10.997276 0.06831955 East Village Chinatown Sun 1AM-5AM
9 9.313165 0.12507373 Battery Park Chinatown Sun 1AM-5AM
10 10.613802 0.11624956 West Village Chinatown Sun 1AM-5AM
모델링 예제
주어진 행동을 모델링하는 것은 매우 복잡한 작업이 될 수 있습니다. 데이터 자체와 비즈니스 요구 사항에 따라 모델에 대한 우리의 선택이 달라지기 때문입니다. 일부 모델은 예측력이 높지만 해석하기가 쉽지 않으며 다른 모델은 반대의 경우가 될 수 있습니다. 또한, 모델을 작성하는 프로세스는, 반복적으로 수행하여 개선하는 방식 보다는, 많은 모델 중에서 선택하는 것과 같은 몇몇 단계와 관련될 수 있기 때문에, 우리는 결정된 모델에 대한 조정 작업을 수행할 수 있습니다.
다음 연습은 RevoScaleR이 제공하는 여러 가지 분석 함수들을 사용하여 고객이 여행에 대해 지급하는 팁의 금액을 예측하는 모델을 만드는 것으로 구성됩니다. 승차 및 하차 지역, 여행 날짜와 시간을 팁 금액에 가장 영향을 주는 변수로 사용합니다.
학습 목표
이 장을 마치게 되면 다음에 대하여 더 잘 이해하게 될 것입니다
- - RevoScaleR을 사용하여 모델을 작성하는 방법
- - 다양한 모델 간의 장단점을 이해
- - 시각화를 사용하여 특정 모델 중에서 결과를 선택하는 프로세스에 대한 가이드
- - (예측을 실행을 통하여) 데이터 셋에 대한 방금 만든 모델을 스코어링하는 방법
이 장은 모델을 실행하고 선택하는 데 꼭 필요한 전반적인 안내서는 아닙니다. 대신에 코드 구현을 예제로 통하여, 최종 목표로 향하기 위한 출발점을 제공합니다.
클러스터 만들기
앞의 그림이 너무 복잡해 보이면, 그 대안으로 k-means 클러스터링을 사용하여 위도와 경도를 기반으로 데이터를 클러스터링 할 수 있습니다. 이 때, 클러스터들에 대하여 동일한 영향이 미치도록 척도(scale)를 조정해야합니다(척도를 재조정하는 간단한 방법은 경도는 -74로, 위도는 40으로 나누는 것입니다). 클러스터가 만들어 지면, 각 클러스터를 구성하는 개별 데이터 포인트 대신에 지도에서 클러스터 중심을 지정하여 표시할 수 있습니다.
xydata <- transmute(mht_sample_df, long_std = dropoff_longitude / -74, lat_std = dropoff_latitude / 40)
start_time <- Sys.time()
rxkm_sample <- kmeans(xydata, centers = 300, iter.max = 2000, nstart = 50)
Sys.time() - start_time
# 중심 좌표에 대해 다시 원래 척도를 적용하여야 합니다.
centroids_sample <- rxkm_sample$centers %>%
as.data.frame %>%
transmute(long = long_std*(-74), lat = lat_std*40, size = rxkm_sample$size)
head(centroids_sample)
Time difference of 2.017159 mins
long lat size
1 -74.01542 40.71149 277
2 -74.00814 40.71107 443
3 -73.99687 40.72133 335
4 -74.00465 40.75183 475
5 -73.96324 40.77466 589
6 -73.98444 40.73826 424
위의 코드 에서는 kmeans 함수를 사용하여 샘플 데이터 세트 mht_sample_df에 대하여 클러스터를 생성 하였습니다. RevoScaleR에는 kmeans 함수에 해당하는 rxKmeans 함수가 있으며, rxKmeans은 data.frame은 물론 XDF 파일에 대해서도 작동합니다. 따라서 rxKmeans를 사용하여 mht_sample_df로 표시된 샘플대신 전체 데이터에 대하여 클러스터를 만들 수 있습니다.
start_time <- Sys.time()
rxkm <- rxKmeans( ~ long_std + lat_std, data = mht_xdf, outFile = mht_xdf,
outColName = "dropoff_cluster", centers = rxkm_sample$centers,
transforms = list(long_std = dropoff_longitude / -74, lat_std = dropoff_latitude / 40),
blocksPerRead = 1, overwrite = TRUE, # need to set this when writing to same file
maxIterations = 100, reportProgress = -1)
Sys.time() - start_time
clsdf <- cbind(
transmute(as.data.frame(rxkm$centers), long = long_std*(-74), lat = lat_std*40),
size = rxkm$size, withinss = rxkm$withinss)
head(clsdf)
Time difference of 2.529844 hours
long lat size withinss
1 -73.96431 40.80540 301784 0.00059328668
2 -73.99275 40.73042 171080 0.00007597645
3 -73.98032 40.76031 198077 0.00005138354
4 -73.98828 40.77187 134539 0.00011077493
5 -73.96651 40.75752 133927 0.00004789548
6 -73.98446 40.74836 186906 0.00005435595
지도 보기
ggmap 패키지를 사용하여 샘플 데이터를 시각적으로 검토해 볼 수 있습니다. 살펴보려는 부분을 충분히 확대하면, 승객이 자주 내리는 경향이 있는 특정한 지역을 볼 수 있습니다.
library(ggmap)
map_13 <- get_map(location = c(lon = -73.98, lat = 40.76), zoom = 13)
map_14 <- get_map(location = c(lon = -73.98, lat = 40.76), zoom = 14)
map_15 <- get_map(location = c(lon = -73.98, lat = 40.76), zoom = 15)
q1 <- ggmap(map_14) +
geom_point(aes(x = dropoff_longitude, y = dropoff_latitude),
data = mht_sample_df, alpha = 0.15, na.rm = TRUE, col = "red", size = .5) +
theme_nothing(legend = TRUE)
q2 <- ggmap(map_15) +
geom_point(aes(x = dropoff_longitude, y = dropoff_latitude),
data = mht_sample_df, alpha = 0.15, na.rm = TRUE, col = "red", size = .5) +
theme_nothing(legend = TRUE)
require(gridExtra)
grid.arrange(q1, q2, ncol = 2)
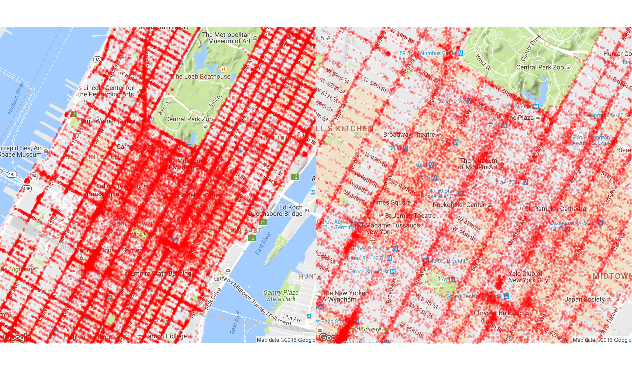
클러스터링 예제
k-means 알고리즘의 병렬 구현인 rxKmeans를 시작으로, 이제 부터 RevoScaleR의 분석 알고리즘을 다소간 살펴 보겠습니다. kmeans 함수와 다르게, rxKmeans는 XDF 파일, 플랫 파일, HDFS 또는 SQL Server에 저장된 데이터에 대하여 실행할 수 있습니다.
앞으로 살펴 보겠지만, 대규모 데이터 세트에 대하여 작업할 때, 알고리즘의 튜닝은 성능에 큰 영향을 줄 수 있습니다.