여러 모델에서 선택
우리가 스스로 물어 보는 질문중 하나는 pickup_dow와 pickup_hour 사이의 상호 작용이 예측 결과에 얼마나 영향을 미치는가 입니다. pickup_nb와 dropoff_nb 사이의 상호 작용 내용만 유지하고 두 번째 상호 작용을 삭제하면 예상치는 얼마나 떨어질까요? 이를 알아보기 위해 우리는 pickup_nb:dropoff_nb만 포함하는 rxLinMod를 사용하여 보다 단순화 된 모델을 만들 수 있습니다. 만들어진 단순 모델로 만들어진 새로운 예측 결과를 cbind를 사용하여 보다 복잡한 모델로 작성한 기존 예측 데이터에 추가합니다.
form_2 <- as.formula(tip_percent ~ pickup_nb:dropoff_nb)
rxlm_2 <- rxLinMod(form_2, data = mht_xdf, dropFirst = TRUE, covCoef = TRUE)
pred_df_2 <- rxPredict(rxlm_2, data = pred_df_1, computeStdErrors = TRUE, writeModelVars = TRUE)
names(pred_df_2)[1:2] <- paste(c('tip_pred', 'tip_stderr'), 2, sep = "_")
pred_df <- pred_df_2 %>%
select(starts_with('tip_')) %>%
cbind(pred_df_1) %>%
arrange(pickup_nb, dropoff_nb, pickup_dow, pickup_hour) %>%
select(pickup_dow, pickup_hour, pickup_nb, dropoff_nb, starts_with('tip_pred_'))
head(pred_df)
pickup_dow pickup_hour pickup_nb dropoff_nb tip_pred_2 tip_pred_1
1 Sun 1AM-5AM Chinatown Chinatown 6.782043 6.796323
2 Sun 5AM-9AM Chinatown Chinatown 6.782043 5.880284
3 Sun 9AM-12PM Chinatown Chinatown 6.782043 6.103625
4 Sun 12PM-4PM Chinatown Chinatown 6.782043 5.913130
5 Sun 4PM-6PM Chinatown Chinatown 6.782043 6.121957
6 Sun 6PM-10PM Chinatown Chinatown 6.782043 6.642192
위의 결과를 통해 단순 모델의 예측 결과값은 탑승 지역과 하차 지역이 같은 조합의 모든 요일과 모든 시간에서 동일하다는 것을 알 수 있습니다. 반면에 기존의 보다 복잡한 모델에 의한 예측 결과값은 4가지 변수의 모든 조합에 대해 고유하게 나타납니다. 즉, pickup_dow:pickup_hour를 모델에 추가하면 예측 결과에 추가적인 변형값이 반영됩니다. 우리는 이 변형값에 중요한 신호가 포함되어 있는지 또는 이것이 어느 정도의 노이즈 값인 경우인지를 알고 싶습니다. 이에 대한 답을 얻기 위해, pickup_dow와 pickup_hour로 나누어서 두 예측의 분포를 비교합니다.
ggplot(data = pred_df) +
geom_density(aes(x = tip_pred_1, col = "complex")) +
geom_density(aes(x = tip_pred_2, col = "simple")) +
facet_grid(pickup_hour ~ pickup_dow)
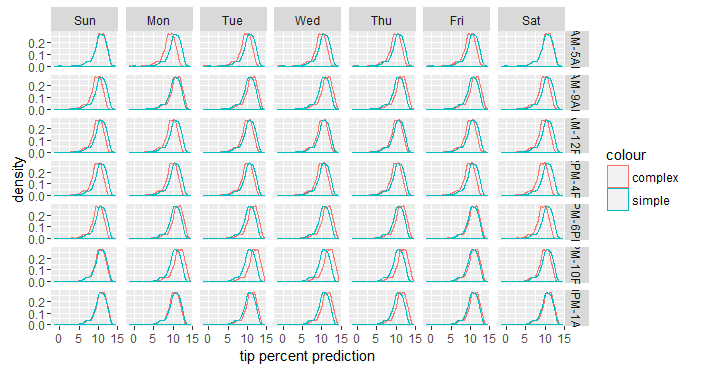
단순화 된 모델에 사용된 두 변수는 예측 결과값에 아무런 영향을 미치지 않기 때문에, 단순 모델은 전체적으로 동일한 분포를 보여 주지만, 더 복잡한 ��델은 pickup_dow 및 pickup_hour의 각 조합에 대해, 일반적으로 분포가 조금 이동한 패턴으로, 약간 다른 분포를 보여줍니다 . 이러한 이동은 두 변수의 각 주어진 조합에서 pickup_dow 및 pickup_hour의 영향도를 나타냅니다. 이러한 이동은 방향성이 있기 때문에(우연이 아님) 중요한 신호(실제적인 중요성은 여전히 논쟁의 여지가 있지만)라고 단정하여도 이상이 없을 것입니다 . 만약 어떤 비즈니스 로직이 적용된다면, 단순화 된 내용을 선택할 수도 있습니다.
팁 예측값을 구간으로 나누어 봅시다. 구간값 선택에 참고하기 위해서, rxQuantile 함수를 사용할 수 있습니다.
rxQuantile("tip_percent", data = mht_xdf, probs = seq(0, 1, by = .05))
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 55% 60% 65% 70% 75% 80%
-1 0 0 0 0 0 0 0 9 12 15 17 17 17 18 18 19
85% 90% 95% 100%
20 21 23 99
위의 결과를 근거로 하여, 8% 미만, 8%~12%, 12%~15%, 15%~18%, 18% 이상인지 여부에 따라 tip_percent를 구분할 수 있습니다. 동일한 정보를 보여주는 막대 그래프를 그릴 수도 있으며, 이럴 경우 해석하기가 조금 더 쉽습니다.
pred_df %>%
mutate_at(vars(tip_pred_1, tip_pred_2), funs(cut(., c(-Inf, 8, 12, 15, 18, Inf)))) %>%
ggplot() +
geom_bar(aes(x = tip_pred_1, fill = "complex", alpha = .5)) +
geom_bar(aes(x = tip_pred_2, fill = "simple", alpha = .5)) +
facet_grid(pickup_hour ~ pickup_dow) +
xlab('tip percent prediction') +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
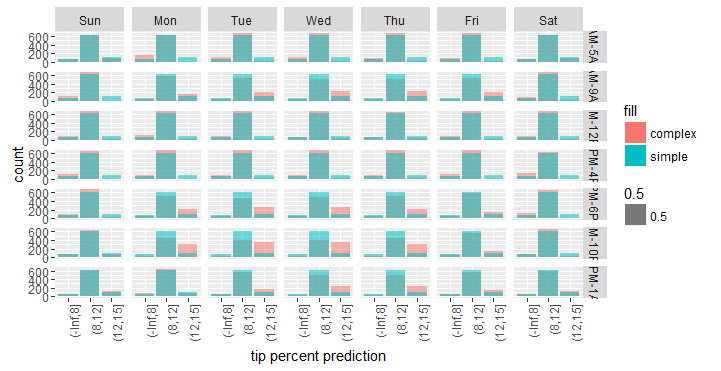
위의 그래프를 보면, 단순화 모델과 비교할 때 복잡한 모델은 특정 요일 및 시간 조합(예:월요일부터 목요일까지러시아워 시간대)에 더 높은 팁을 지불하는 승객과 평균보다 낮은 승객수를 예측하는 경향이 있음을 알 수 있습니다.